sortedset¶

class blist.sortedset(iterable=(), key=None)¶

A sortedset provides the same methods as a set. Additionally, a sortedset: maintains its items in sorted order, allowing the sortedset to be indexed.

An optional iterable provides an initial series of items to populate the sortedset.

key specifies a function of one argument that is used to extract a comparison key from each set element: key=str.lower. The default value is None (compare the elements directly). The key function must always return the same key for an item or the results are unpredictable.

Unlike a set, a sortedset does not require items to be hashable.

A sortedset can be used as an order statistic tree (Cormen et al., Introduction to Algorithms, ch. 14).

x in S

Returns True if and only if x is an element in the set.

Requires 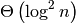$\Theta\left(\log^2 n\right)$ total operations or 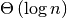$\Theta\left(\log n\right)$ comparisons.

Return type:	`bool`

del S[i]

Removes the element located at index i from the set.

Requires 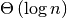$\Theta\left(\log n\right)$ operations and no comparisons.

del S[i:j]

Removes the elements from i to j from the set.

Requires 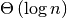$\Theta\left(\log n\right)$ operations and no comparisons.

S < S2

Test whether the set is a proper subset of S2, that is, S <= S2 and S != other.

In the worst case, requires 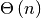$\Theta\left(n\right)$ operations multiplied by the cost of S2‘s in operation.

Return type:	`bool`

S > S2

Test whether the set is a proper superset of S2, that is, S >= S2 and S != S2.

In the worst case, requires 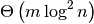$\Theta\left(m \log^2 n\right)$ operations or 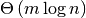$\Theta\left(m \log n\right)$ comparisons, where m is the size of S2 and n is the size of S.

Return type:	`bool`

S[i]

Returns the element at position i.

Requires 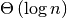$\Theta\left(\log n\right)$ operations in the worst case but only 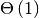$\Theta\left(1\right)$ operations if the set’s size has not been changed recently. Requires no comparisons in any case.

(Cormen et al. call this operation “SELECT”.)

Return type:	item

S[i:j]

Returns a new sortedset containing the elements from i to j.

Requires 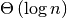$\Theta\left(\log n\right)$ operations and no comparisons.

Return type:	`sortedset`

S *= k

Increase the length of the set by a factor of k, by inserting k-1 additional shallow copies of each item in the set.

Requires 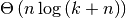$\Theta\left(n \log\left(k + n\right)\right)$ operations and no comparisons.

iter(S)¶

Creates an iterator over the set.

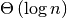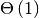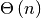Requires $\Theta\left(\log n\right)$ operations to create the iterator. Each element from the iterator requires $\Theta\left(1\right)$ operations to retrieve, or $\Theta\left(n\right)$ operations to iterate over the entire set.

Return type:	iterator

len(S)¶

Returns the number of elements in the set.

Requires 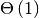$\Theta\left(1\right)$ operations.

Return type:	`int`

S * k or k * S

Returns a new sorted set containing k shallow copies of each item in S.

Requires 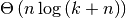$\Theta\left(n \log\left(k + n\right)\right)$ operations and no comparisons.

Return type:	`sortedset`

reversed(S)¶

Creates an iterator to traverse the set in reverse.

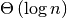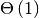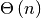Requires $\Theta\left(\log n\right)$ operations to create the iterator. Each element from the iterator requires $\Theta\left(1\right)$ operations to retrieve, or $\Theta\left(n\right)$ operations to iterate over the entire set. Requires no comparisons in any case.

Return type:	iterator

S.add(value)¶

Add the element value to the set.

Requires 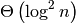$\Theta\left(\log^2 n\right)$ total operations or 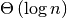$\Theta\left(\log n\right)$ comparisons.

L.bisect_left(value)¶

Similarly to the bisect module in the standard library, this returns an appropriate index to insert value in L. If value is already present in L, the insertion point will be before (to the left of) any existing entries.

Requires 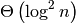$\Theta\left(\log^2 n\right)$ total operations or 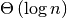$\Theta\left(\log n\right)$ comparisons.

L.bisect(value)¶: Same as bisect_left.

L.bisect_right(value)¶: Same thing as bisect_left, but if value is already present in L, the insertion point will be after (to the right of) any existing entries.

S.clear()¶

Remove all elements from the set.

Requires 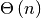$\Theta\left(n\right)$ total operations and no comparisons in the worst case.

S.copy()¶

Creates a shallow copy of the set.

Requires 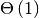$\Theta\left(1\right)$ total operations and no comparisons.

Return type:	`sortedset`

S.count(value)¶

Returns the number of occurrences of value in the set.

Requires 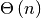$\Theta\left(n\right)$ operations and 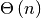$\Theta\left(n\right)$ comparisons in the worst case.

Return type:	`int`

S.difference(S2, ...)¶

S - S2 - ...

Return a new set with elements in the set that are not in the others.

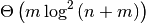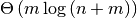In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the combined size of all the other sets and n is the size of S.

Return type:	`sortedset`

S.difference_update(S2, ...)¶

S -= S2 | ...

Update the set, removing elements found in keeping only elements found in any of the others.

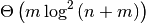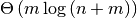In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the combined size of all the other sets and n is the initial size of S.

S.discard(value)¶

Removes the first occurrence of value. If value is not a member, does nothing.

In the worst case, requires 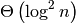$\Theta\left(\log^2 n\right)$ operations and 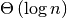$\Theta\left(\log n\right)$ comparisons.

S.index(value[, start[, stop]])¶

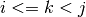Returns the smallest k such that $S[k] == x$ and $i <= k < j$ . Raises ValueError if value is not present. stop defaults to the end of the set. start defaults to the beginning. Negative indexes are supported, as for slice indices.

In the worst case, requires 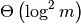$\Theta\left(\log^2 m\right)$ operations and 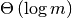$\Theta\left(\log m\right)$ comparisons, where m is stop - start.

(Cormen et al. call this operation “RANK”.)

Return type:	`int`

S.intersection(S2, ...)¶

S & S2 & ...

Return a new set with elements common to the set and all others.

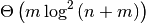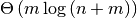In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the combined size of all the other sets and n is the size of S.

Return type:	`sortedset`

S.intersection_update(S2, ...)¶

S &= S2 & ...

Update the set, keeping only elements found in it and all others.

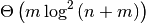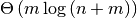In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the combined size of all the other sets and n is the initial size of S.

S.isdisjoint(S2)¶

Return True if the set has no elements in common with S2. Sets are disjoint if and only if their intersection is the empty set.

Return type:	`bool`

S.issubset(S2)¶

S <= S2

Test whether every element in the set is in S2

In the worst case, requires 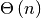$\Theta\left(n\right)$ operations multiplied by the cost of S2‘s in operation.

Return type:	`bool`

S.issuperset(S2)¶

S >= S2

Test whether every element in S2 is in the set.

In the worst case, requires 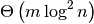$\Theta\left(m \log^2 n\right)$ operations or 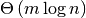$\Theta\left(m \log n\right)$ comparisons, where m is the size of S2 and n is the size of S.

Return type:	`bool`

S.symmetric_difference(S2)¶

S ^ S2

Return a new set with element in either set but not both.

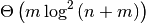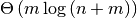In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the size of S2 and n is the size of S.

Return type:	`sortedset`

S.symmetric_difference_update(S2)¶

S ^= S2

Update the set, keeping only elements found in either set, but not in both.

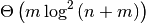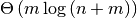In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the size of S2 and n is the initial size of S.

S.pop([index])¶

Removes and return item at index (default last). Raises IndexError if set is empty or index is out of range. Negative indexes are supported, as for slice indices.

Requires 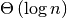$\Theta\left(\log n\right)$ operations and no comparisons.

Return type:	item

S.remove(value)¶

Remove first occurrence of value. Raises ValueError if value is not present.

In the worst case, requires 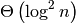$\Theta\left(\log^2 n\right)$ operations and 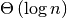$\Theta\left(\log n\right)$ comparisons.

S.union(S2, ...)¶

S | S2 | ...

Return a new sortedset with elements from the set and all others. The new sortedset will be sorted according to the key of the leftmost set.

Requires 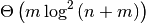$\Theta\left(m \log^2 \left(n + m\right)\right)$ operations or 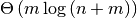$\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the total size of the other sets and n is the size of S.

Return type:	`sortedset`

S.update(S2, ...)¶

S |= S2 | ...

Update the set, adding elements from all others.

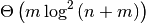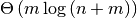In the worst case, requires $\Theta\left(m \log^2 \left(n + m\right)\right)$ operations and $\Theta\left(m \log\left(n + m\right)\right)$ comparisons, where m is the combined size of all the other sets and n is the initial size of S.

sortedset¶

Table of contents

blist

heapdict

winreg_unicode

ion-sampler

Navigation

sortedset¶

Table of contents

blist

heapdict

winreg_unicode

ion-sampler

Quick search

Navigation